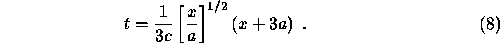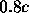 . Show that in the frame of the
garage, the whole car can indeed enter the garage before its front
strikes the wall. Also calculate the length of the garage as seen by
the driver and prove that he expects to strike the wall
. Show that in the frame of the
garage, the whole car can indeed enter the garage before its front
strikes the wall. Also calculate the length of the garage as seen by
the driver and prove that he expects to strike the wall 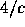 seconds
before the back of the car gets in through the back of the garage.
Recalling that the maximum speed of propagation of information is
c, explain how the car fits into the garage before the news that
the front of the car has hit the garage wall reaches the back of the
car.
seconds
before the back of the car gets in through the back of the garage.
Recalling that the maximum speed of propagation of information is
c, explain how the car fits into the garage before the news that
the front of the car has hit the garage wall reaches the back of the
car.
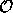 is given by
is given by

Show that for an observer at rest relative to 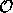 [ i.e. with a
four- velocity
[ i.e. with a
four- velocity 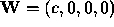 ], the particle's three- velocity
], the particle's three- velocity 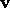 can be written as
can be written as
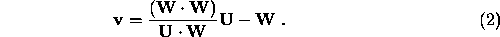
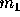 moving with velocity
moving with velocity 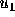 along the x- axis collides elastically with a stationary particle of
rest mass
along the x- axis collides elastically with a stationary particle of
rest mass 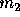 and as a result
and as a result 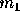 and
and 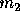 are deflected through
angles
are deflected through
angles 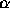 and
and 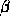 respectively. If E and
respectively. If E and 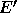 are the
total energies of the particle
are the
total energies of the particle 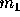 before and after the collision
respectively, show that
before and after the collision
respectively, show that
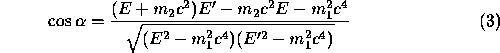
 and the four-
acceleration
and the four-
acceleration 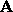 of a particle in Special Relativity and specify how
they relate to the Newtonian velocity
of a particle in Special Relativity and specify how
they relate to the Newtonian velocity 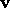 and Newtonian acceleration
and Newtonian acceleration
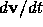 . If the rest mass of the particle is
. If the rest mass of the particle is 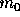 , what is its
four- momentum
, what is its
four- momentum 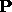 ?
?
A particle moves with variable velocity 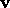 relative to some inertial
frame, under the action of a force
relative to some inertial
frame, under the action of a force 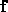 . Show that
. Show that
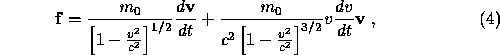
where v is the magnitude of 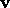 . Infer that
. Infer that
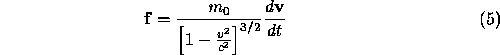
if the acceleration is parallel to 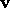 , while
, while
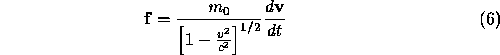
if the acceleration is perpendicular to 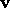 .
.
Suppose the particle moves along the x- axis under a force of magnitude
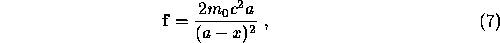
being at rest at t=0. Show that the time taken to move to the point with
coordinate 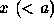 is
is